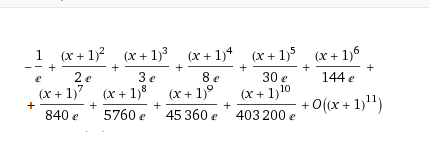Остаточный член в форме пеано
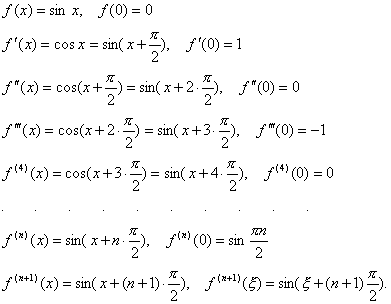
Формула Тейлора с остаточным членом в форме Пеано, Лагранджа
Применим метод математической индукции. Из равенств 2 и 3 получаем:. Боярчук "Функции комплексного переменного: теория и практика" Справочное пособие по высшей математике.













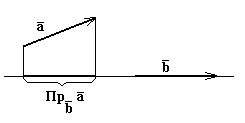
Формула называется формулой Тейлора с центром в точке a; - остаточный член в формуле Тейлора в общем виде. Рассмотрим вспомогательную функцию. Остаточный член в форме Тейлора представляет собой б. Бесплатная лекция: " Лекция 3 " также доступна. Такую запись остаточного члена называют ост. В форме Пеано:.



Перейти к основному содержанию. Вы используете гостевой доступ Вход. Остаточный член в форме Пеано Остаточный член в форме Пеано. Формула Тейлора с остаточным членом в форме Пеано. Нажмите на ссылку Остаточный член в форме Пеано , чтобы открыть ресурс. Перейти на